This article appeared in the Horololgical Science Newsletter in June of 2000. Since then I have added an optional temperature sensor to MicroSet. This will allow the computer software to record temperature and rate at the same time, making temperature studies much easier.
We know that temperature affects the rate of our clocks and watches. The question is, how can we measure it accurately? The traditional method of comparing a clock to a precision reference once a day leaves a lot to be desired. Not only does it take a very long time to get results, but the resolution of the readings is very coarse as well.
I have been using the MicroSet Clock and Watch Timer to study thermal response of various timekeepers for a couple of years. It's an easy way to get both high precision and high accuracy in thermal studies. The following article will explain the application and limits of using MicroSet to measure temperature compensation.
MicroSet will plot a graph of the rate of a clock over time. If we let the graph develop over 24 hours we can see the day-to-night thermal cycle of the clock. Figure 1 shows such a graph made with a common Hermle short pendulum movement with a metal rod. The clock was sitting in my living room in Santa Barbara in May. The daytime temperature was in the neighborhood of 75 degrees, the nights were closer to 60 degrees. The peaks in the graph (fastest rate) occur around six AM, when the house is at its lowest temperature. The slow troughs represent the warm afternoons.
The range of change can be seen to be about four grid lines, with each line representing a rate change of 22.3 seconds per day. In other words, this Hermle changes rate by about a minute and a half per day depending on room temperature. If you use a precision timer to adjust the rate of this clock, you can get into trouble by doing it on a hot afternoon because the rate at that instant is not representative of the average.
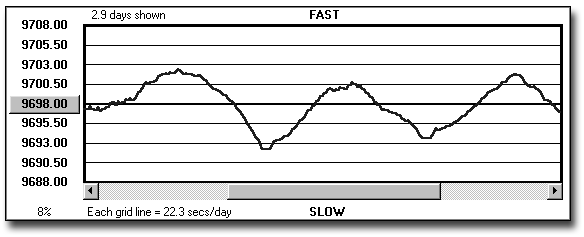
Figure 1 - Temperature effect on a Hermle movement
Watches are also vulnerable to temperature changes. Figure 2 shows the rate of a Doxa pocket watch over four hours. During this time I shined a bright work light on the watch to warm it up. It, too, shows a rate change with temperature. The variance here is on the order of a minute per day over the temperature change (I did not quantify the change with a thermometer). I have also seen pocket watches slow down as they were made warmer.
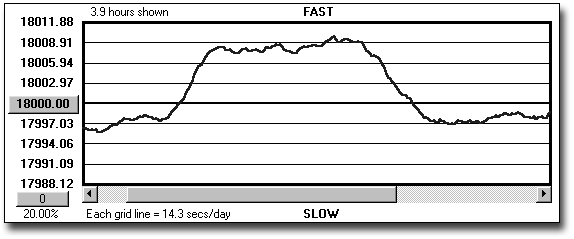
Figure 2 - Temperature effect on a pocket watch
I have made several experimental pendulum clocks with electromagnetic impulse. In these clocks the pendulum is made to swing with a magnetic impulse, and no mechanical linkage connects the pendulum to a movement (the dial is an electric slave). In these clocks the pendulum is "free" to swing at a pure rate, undisturbed by friction in a movement, but vulnerable to environmental factors like temperature and atmospheric pressure. Temperature is, by far, the dominant influence. I use invar for the pendulum rod and a brass cylinder two inches in diameter and six inches tall for the bob. I have tried to get these two materials to compensate each other for thermal changes, with imperfect results. My measurements indicate that I'm still slightly under compensated. I have also supported the brass bob on an aluminum sleeve to attempt greater compensation, but my calculations indicate that six inches of brass bob is just not enough to overcome the length of a seconds beating invar rod.
I might point out that I have found that my calculations of thermal response do not match my empirical measurements. My conclusion is that the real world is much more complex than my spreadsheets. If you are building temperature compensation mechanisms by theory, my advice is to take a close experimental look at the result because it may be somewhat different that you expect.
Figure 3 shows a graph of my last experimental clock over several days. The rate change seen in this graph is much smaller than what we have previously seen, though I have configured the program to "zoom in" on the data to display the change more clearly. Here the fluctuations cover about five grid lines, each of which represents a rate change of 0.1 seconds per day. This produces a 24-hour fluctuation in rate of about 1/2 second due to ambient temperature change. Note also that we can see a complex shape in the response. This is due to the complexities of the complete system; different mass in the bob and rod, the insulated wooden clock case, whether or not the furnace turns on or the sun shines in. MicroSet makes it easy to capture and display these short term changes.
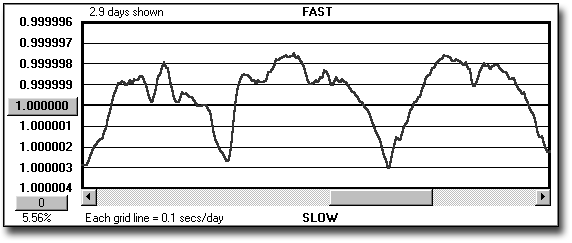
Figure 3 - Experimental pendulum
The values assigned to the Y axis in Figure 3 show that the beat time varies by about +/- three microseconds. We are now into the realm where we may become suspicious of the MicroSet timer. It uses an uncompensated quartz crystal for a timebase, and, though I calibrate each timer to an accuracy of +/- one part per million, the rate of oscillation of the quartz crystal will fluctuate with temperature. I have quantified the error in the crystal in the same way that I study clocks; by logging a rate with MicroSet. The rate that I log is the one second pulse of either a GPS receiver or a rubidium reference oscillator. We know that the output of these two sources is exactly one second to better than six decimal places. So any change in this value recorded by MicroSet will be the change in MicroSet's internal crystal oscillator. I was going to prepare a graph of this change over a 24-hour cycle, but it was a very dull graph. The timebase in MicroSet varied by just +/- one microsecond in 24 hours. So this is the practical limit of resolution of MicroSet over modest changes in ambient room temperature.
Though the thermal error in MicroSet is small, if we wish to measure temperature effects that are as small as a few microseconds, we must remove this error. This can be done by using a MicroSet accessory called the "GPS Interface". This device allows MicroSet to take measurements of precision clocks by measuring the difference between a precision seconds source (like a GPS receiver) and the clock. In this mode MicroSet measures the drift of the clock over time. Commands in the interface software can convert the drift readings into rate information if that is preferred. Though the absolute value of the difference measured by MicroSet may still be vulnerable to a two or three part per million fluctuation, this error is not cumulative and every reading is resynchronized to a reference that is immune to local temperature change. The thermal fluctuation within MicroSet becomes insignificant.
Update: February 25, 2001
I have recently finished the design of a Temperature Compensated Crystal Oscillator (TCXO) which can be installed in MicroSet to provide temperature stable readings on all measurements. The specifications claim an error of +/- 2.5 parts per million over a temperature range of -30 to +75 degrees Centigrade. The variance over small changes encountered in living rooms where clocks are kept is better than one part per million. The TCXO oscillator can be added to recent models of MicroSet 2 or MicroSet 3.
Bryan Mumford
Santa Barbara, California