It is said that two clocks, running on the same wall, will interfere with each other. I can clearly show that this is true.

This picture shows a Synchronome clock next to an experimental pendulum. Each pendulum is tuned near a one second beat time, though the experimental pendulum is slow by about 28 seconds per day.

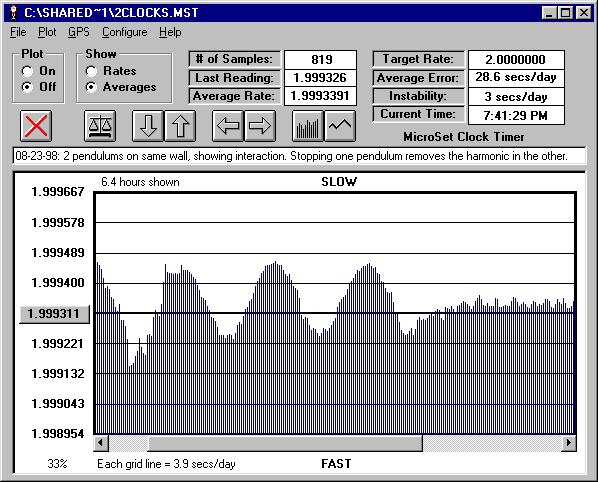
The graph below shows the rate (measured with the MicroSet Clock Timer) on the experimental pendulum. You will see that it speeds up and slows down in a very regular manner for most of the 6.4 hours shown. This change in rate is relatively large, on the order of 10 seconds per day, and it is caused by interference with the Synchronome pendulum. Mid-way through the graph I stopped the Synchronome pendulum, and the disturbance disappears.

The frequency of the disturbance has to do with the difference in rate between the two pendulums. The experimental one is running fast by about 28 seconds per day. That means a little more often than once an hour the two pendulums will come into phase with each other. When they are in phase, the oscillations reinforce each other, the amplitude increases, and the clocks slow down. When they are exactly out of phase, the oscillations tend to dampen, the amplitude decreases, and the rate increases. Note that the rate adopted by the pendulum after I stopped the Synchronome is about half way between the slowest and the fastest rates during the oscillation. The period of oscillation is a little more often than once per hour.

This effect was so dramatic I began to wonder if it might also effect a more serious experimental clock. This clock hangs on the same wall as a Self Winding Model 41, which has a relatively heavy mercury filled bob. Both clocks beat seconds, both are quite accurate, and both are timed quite close to rate. Recent results with my experimental clock showed that it ran for about a week and a half with a total loss of .02 seconds, but then began to drift and lost a whole second in the next week.

I adjusted the voltage in the drive circuit to bring it precisely back to rate, and it ran fine for about a week. Then it began to lose.

One morning I looked at the pendulums of the Self Winding and my experimental clock. My own clock was gaining. The pendulums were very nearly in phase, with the Self Winding a little behind. Was it possible that this motion could traverse the 10 or 15 feet between them and retard the swing of the experimental pendulum, drawing energy out of it, decreasing the amplitude, and increasing the rate? I fiddled with the Self Winding and got it to swing exactly in phase with the experimental pendulum. Within 10 minutes the experimental clock TURNED AROUND and began to lose! I started and stopped the Self Winding several times to convince myself this was really happening, and it was. The coupling between these two pendulums was much less than that in the previous example, but more pronounced than the thermal drift in the experimental clock. My clock was evidently more accurate than I first thought, but when the two clocks drifted into phase, my pendulum would swing wider and the clock would slow down. It took a whole week for this disturbance to manifest because the two clocks were tuned very closely to the same rate. I expect that the difference between them was about 1 second per week, because it took about a week for the rate change to occur.

The following graph shows the subtle change in my experimental clock caused by the Self Winding's pendulum. The rate is very near 1.000001 seconds per beat, but there is a hump at the beginning and end of the sample period. This hump was produced by starting the pendulum of the Self Winding clock in phase with the pendulum of the experimental clock. Between the humps, the Self Winding pendulum was stopped. The rate change is subtle, to be sure. But it amounts to about one and a half microseconds per beat, which is about one second per week of error.

I might mention that there is no way we would be able to see this effect without the GPS interface to MicroSet. These rate changes are smaller than the limit of precision in the timer itself. But by referencing the GPS precision seconds signal, you can reliably resolve drift as small as 20 or 30 microseconds over a week, a month, or any interval you choose.

For reference:
Both clocks are fastened to the wall. The Self Winding is bolted very solidly top and bottom. The experimental clock just hangs on a bracket from a single bolt in the wall. The wall is an interior load bearing wall, with wooden studs and drywall sheeting. The wall stands on a poured concrete footing directly beneath it.

---

Bryan Mumford
Santa Barbara, California
August 25, 1998

Home   |   Horology