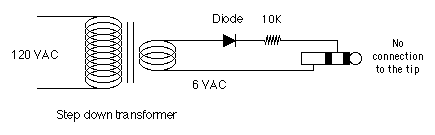
Measuring the accuracy of 60 cycle power The frequency of AC power has been used to run clocks since the 1920s. In the early days these clocks were not very accurate because the power generators were not accurately controlled. Henry Warren wanted to sell AC powered clocks, and he invented a special clock that power companies could use to keep their generators more accurate. Today the AC power grid is a complicated system that's highly controlled. But how accurate is it really? To answer this question I set up a MicroSet Clock Timer to measure the accuracy of the 60 cycles. If the 60 cycles run fast, so will any clock that keeps time with them. Detecting the 60 cycle power is easy. If you have a MicroSet 3, you can do this yourself. Get a low voltage transformer that puts out 6 volts or less. Connect a diode to one side of the output. Connect a 10K resistor to the other end of the diode. Connect the other end of the resistor to the middle terminal of the MicroSet sensor jack. Connect the base of the MicroSet sensor jack to the other side of the transformer output.
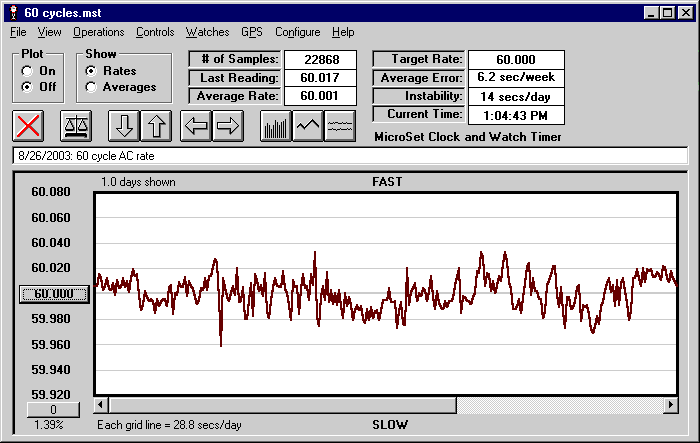
To measure the 60 cycle rate, you must have MicroSet 3 with the Accutron mode. This was designed to measure Accutron watches with a tuning fork frequency around 400 cycles per second, but it can also measure 60 cycles per second. When you first enter the Accutron mode, MicroSet will try to show you the rate of the AC frequency as seconds of error per day. This is of no use for our purpose. Press the MINUS button and MicroSet will show you the rate as cyles per second to three decimal places. The graph below is 24 hours of the 60 cycle power in Santa Barbara on August 26 of 2003. This graph is typical of what I've observed. The frequency changes throughout the day. Each horizontal line in the graph represents a rate change equivalent to almost 29 seconds per day. The fluctuations in frequency span almost two grid lines. So the rate at any instant may be fast or slow by almost a minute per day. An AC clock will never show such errors, of course, because a clock shows the average rate. The average error over these 24 hours was 6.2 seconds per week.
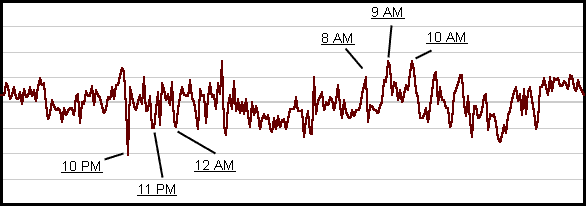
One interesting thing I observed in the data is that the rate is likely to spike each hour. In the graph below I've marked the peaks with the times they occurred.
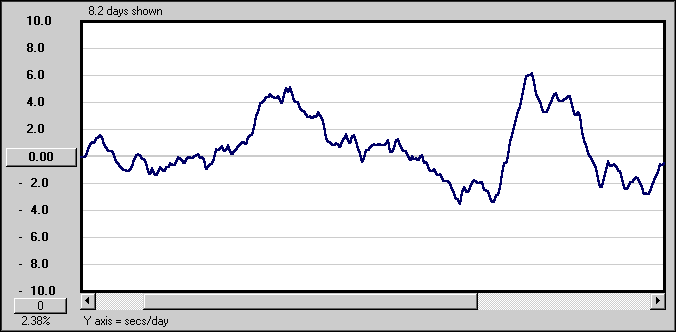
But what of timekeeping? The following graph (a boxcar average of 24 hours) shows how fast or slow an AC clock would be over any 24 hour period. It can be seen that on some 24 hour periods the clock might be as slow as six seconds or as fast as four seconds (the fast and slow positions are inverted in this graph). The fastest frequency I recorded was 60.047 Hz and the slowest was 59.954 Hz. The total error I measured over 9.6 days was slow by 3.57 seconds.
Bryan Mumford
|